解调PWM信号
脉宽调制(PWM)被广泛应用于开关电源和电机控制器。分析控制环路的动态情况要求观察脉冲宽度随时间的变化。如果你的示波器具有电源分析选件包,那么你就能直接使用这个功能。如果你的示波器没有这方面的配置,你可以使用示波器的跟踪(某些示波器中的时间跟踪)功能解调出PWM控制信号。
首先,确保你的示波器包含所有实例测量。也就是说,如果你测量波形的宽度,示波器将测量屏幕上出现的波形的每个周期。示波器还应该包含依据测量到的参数产生波形的跟踪功能。宽度或“width@level”参数的跟踪可以显示每个周期脉宽随时间的变化,并且与源轨迹同步。因此宽度跟踪是解调PWM信号的理想工具。跟踪功能可以从参数或数学设置中访问。
图1显示了作为负载电流阶跃变化(轨迹C2,从上数第3个)响应的PWM控制器输出(轨迹C1,顶部轨迹)的跟踪轨迹F1,即展示width@level 参数与时间关系的(底部轨迹)。缩放轨迹Z1(从上数第2个)是水平方向放大了的随负载变化的控制器输出,展示了脉宽的变化。
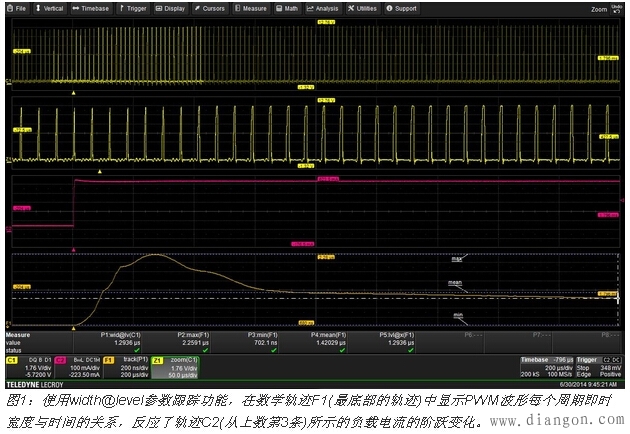
参数可以像图1中那样应用于跟踪功能,其中参数P2到P4分别从跟踪波形中读取最大、最小、平均和最后一个脉冲宽度。
创建用于评估磁性器件的磁滞图
用于电感或变压器等电磁元件的磁滞或B/H曲线是一种常见的电源测量项目。磁性材料可以通过绘制作为磁场强度(H)函数的磁通密度(B)进行表征。这个功能有时在示波器的电源分析选件中提供。这种图也很容易在带X-Y显示器的任何示波器上创建。图2显示了如何连接电感和信号发生器产生B/H曲线。
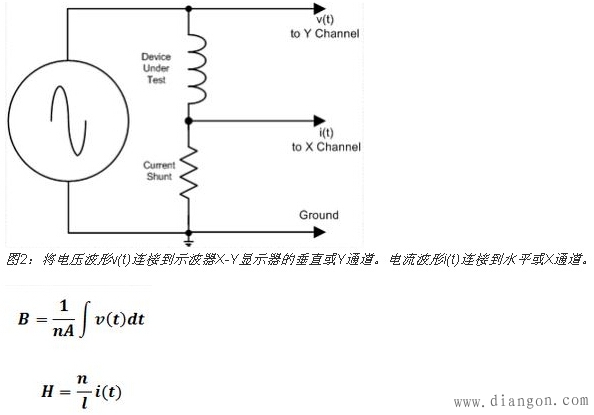
H是磁场强度,单位为安培/米
B是磁通密度,单位特斯拉
A是横截面积,单位平方米
n是匝数
l是平均路径长度,单位米
v(t)是电感上的电压,单位伏特
i(t)是流过电感的电流,单位安培
需要注意的是,为了确定磁通密度,必须对电压波形求积分。
如果需要的话,你可以使用重定标数学函数对磁场强度和磁通密度进行调整。这要求掌握待测器件的物理特性知识,如上面公式中规定的那样。
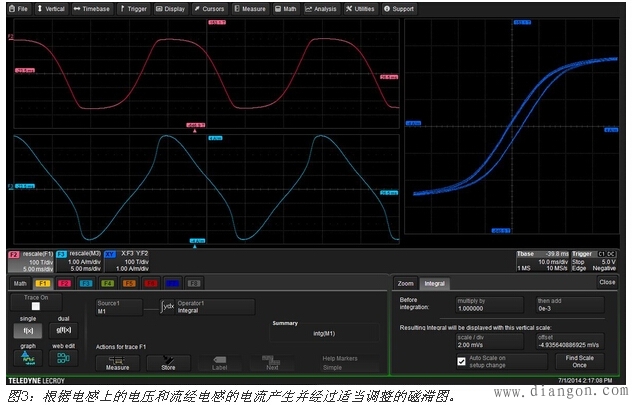
图3显示了这种电压与电流经积分后的B/H曲线在示波器屏幕上显示的结果。从待测器件施加的电压用数学轨迹F1进行积分,并在数学轨迹F2中作了重新定标,最终在X-Y显示器的垂直轴上读取单位为特斯拉的磁通密度。电流波形在数学轨迹F3中得到重新定标,并应用于水平轴。
将波形数据重定标为合适的单位
在前一章节中,我们必须将电压波形的积分转换为磁通密度。这要求将波形除以一个常数(匝数与横截面的乘积)。另外,正确的单位应该是特斯拉。这些操作可以使用示波器的重定标数学函数来完成。重定标允许用户将波形乘上一个常数,然后再增加一个常数,而且可以通过配置用用户选择的单位覆盖原有单位(本例中是伏特)。本例中使用的示波器提供48种标准电气单位,包括特斯拉。
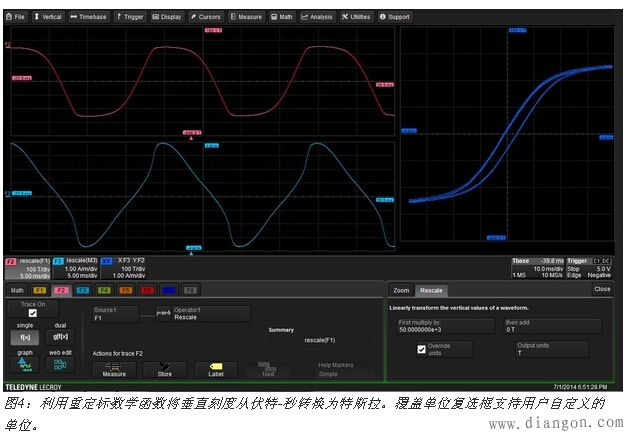
图4显示了数学轨迹F2的重定标设置。我们需要将电压波形的积分除以20×10-6,但因为重定标函数只提供与常数的相乘,因为我们需要使用倒数或50×103。覆盖单位复选框打上勾后会提供一个单位输入域,我们在此输入代表特斯拉的T。这样将波形中的每个点乘以想要的常数就可以实现积分输出(数学轨迹F1)的重定标。F2数学轨迹的垂直坐标现在的读取单位就是特斯拉了。同样,数学轨迹F3用于将测量得到的电流重定标为磁场强度。
创建带通滤波器
你曾经有过用带通滤波器将目标信号与相邻通道干扰隔离开来的需求吗?大多数中档示波器都包含有增强分辨率(ERES)数学函数形式的低通滤波器,但没有带通滤波器,除非你有数字滤波器选件。你可以使用一些技巧将ERES低通滤波器转换成带通滤波器。图5显示了这一技巧。
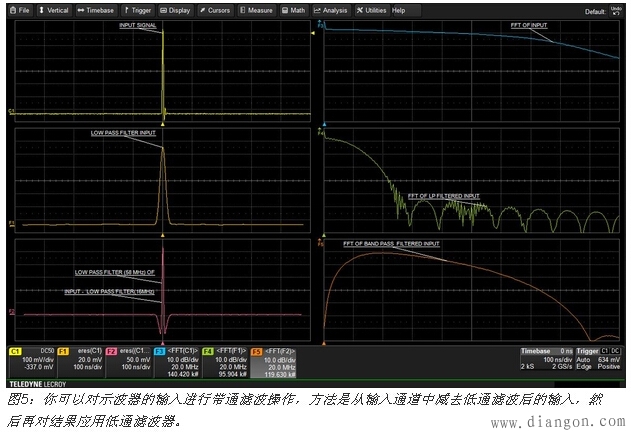
左上角的轨迹C1是一种窄脉冲输入信号。设置好的数学函数F1用于对通道1的输入进行低通滤波。在这个案例中,ERES滤波器是16MHz的低通滤波器。轨迹F1(左边中间)显示了滤波器对时域信号的影响。在数学函数F2中,从输入中减去F1中低通滤波器的输出,从而去除低频内容,得到高通响应。F2中的第二次数学操作是另外一个截止频率为58MHz的ERES低通滤波器。结果就是轨迹F2(左下)中的带通响应。
轨迹F3(右上)显示了输入快速傅里叶变换(FFT)的频谱。F4(右中)是低通滤波过后的输入频谱。轨迹F5(右下)是带通滤波操作的频谱。对这些滤波器的控制受ERES函数中滤波器选择的限制。示波器中提供的数字滤波器选件包可以提供更大的灵活性,但这种小技巧在标准配置的示波器中都可以使用。
捕捉串行数据图案
示波器一般都有几种工具捕捉串行数据图案。可选的串行触发器和解码功能可以根据规定的串行标准对数据进行操作。另外一种串行图案捕捉技术是使用案例所用示波器中被称为WaveScan的示波器搜索功能。这种数据搜索引擎包含在所有这家供货商的中档示波器中,其它制造商也提供类似的功能。图6显示了使用WaveScan捕捉串行图案的例子。
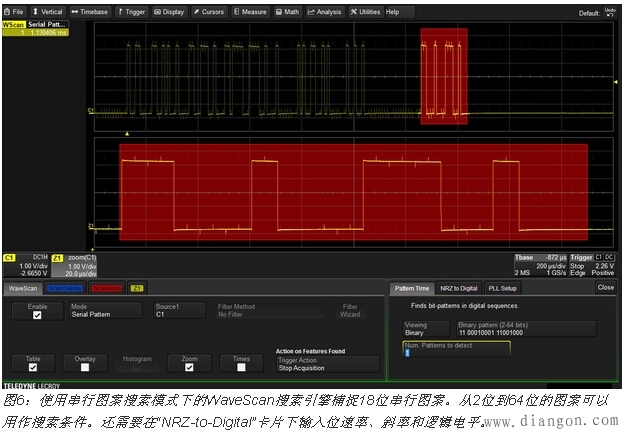
串行图案搜索模式将根据输入的二进制或16进制长度值搜索从2位至64位的图案。除了串行图案外,用户还必须输入串行位速率。这些参数包含在“NRZ-to-Digital”卡片内用于串行图案识别的物理参数设置中,除了数据位速率,还有斜率和数据的逻辑阈值。
当检测到所选的图案时,WaveScan的7个动作中任何一个都可以被触发。图6所示例子已经停止了采集。
发现信号异常
全部实例测量是示波器基于采集波形每个周期进行时序测量的能力。如果你测量每个周期,你可以显示跟踪图,用于展示被测参数随时间的变化,而该变化与采集的信号输入是完全同步的。图7包含这一功能的例子。
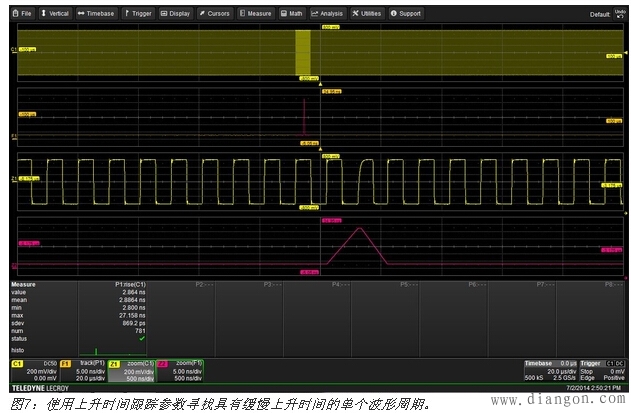
采集信号是一个具有781个周期的4MHz正弦波。从上升时间参数(P1)统计数据看,我们可以发现每个周期要做一次测量,因此共有781个值。上升时间的平均值是2.88ns。最小值是接近平均值的2.8ns,但最大值是27ns。打开上升时间跟踪曲线数学轨迹F1,我们可以在轨迹中心附近看到一个峰值。跟踪图显示了随时间变化的每个周期测量值。它在时间上与轨迹C1中所采集的波形是同步的。跟踪到的上升时间最大值是27ns。其位置与具有缓慢上升时间的周期在时间上是同步的。
将缩放轨迹Z1和Z2分别用作C1和F1的缩放图,同时应用多次缩放功能进行水平跟踪,我们可以扩展它们寻找到对应于最大周期值的单个周期。
这是全部实例测量的优势。你可以见到以单个周期为基础的波形时序变化。这种技术可以代替使用WaveScan搜索功能寻找具有缓慢上升时间的这种脉冲。
噪声测量工具
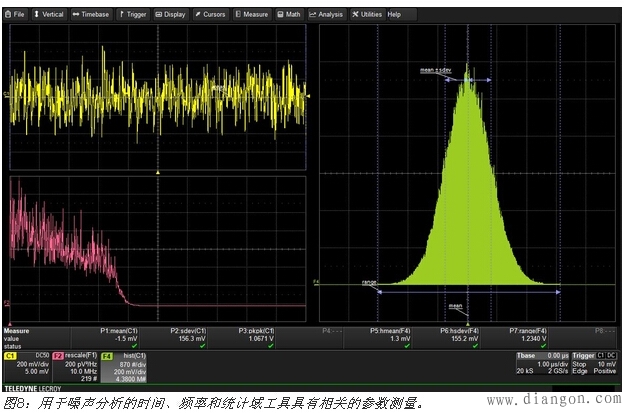
随机过程很难表征,因为没有哪次测量能够提供有关前次或下次测量的任何信息。只有通过观察累积测量结果才能了解到你正在研究的过程。图8显示了用于测量噪声等随机过程的基本工具。左上方的轨迹是通道1输入信号的幅度时间图。左下方的轨迹是功率谱密度图,显示的是噪声功率的频率分布情况。右边的轨迹是单次噪声电压测量的柱状图。这个柱状图显示了单次测量的幅值分布情况。这些分析功能与测量参数一起为噪声测量提供了完整的工具集。
你可以通过使用测量参数了解随机噪声信号的特征。用于噪声测量的最有意义的参数是波形的平均值(P1)、标准偏差(P2)和峰峰值(P3)。在这些测量参数中,也被称为交流均方根值的标准偏差可能是最有用的,因为它描述了波形的有效值。
频域中最常见的噪声测量是功率谱密度(PSD)。PSD的测量单位通常是V2/Hz,代表了单位带宽的功率大小。因为噪声一般在频谱上是展开的,因此一个频段或一定范围频率内的噪声功率可以通过在该范围频率内对PSD积分来确定。
柱状图为用户提供了待测过程的概率密度函数的估计。这个数据可以用柱状图参数来解释。图8显示了三个柱状图参数,即柱状图平均值(P5中的hmean)、柱状图标准偏差(P6中的hsdev)和范围(P7)。这些是柱状图分布的均值、标准偏差和范围。这三张图可以快速表征噪声。
三相功率测量
用于测量三相电路功率的双功率计方法可以用四通道示波器来实现。三线三相负载的功耗可以用一个四通道示波器来确定,方法是测量两个相位电流和两个线路电压。举例来说,观察图9所示原理图,三相电机消耗的总功率可以通过测量Vac、Vbc、Ia,和Ib加以确定:
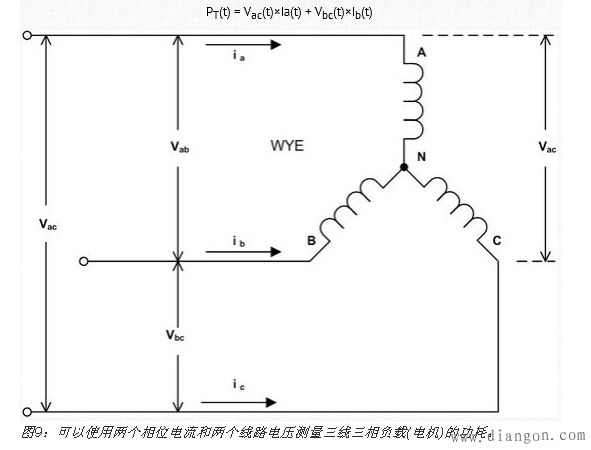
线路电压Vac(t) 和Vbc(t)是用高压差分探头测量的。相位电流Ia 和Ib是用电流探头测量的。这种功率测量要求使用带4个输入通道的示波器。图10描述了这种技术。
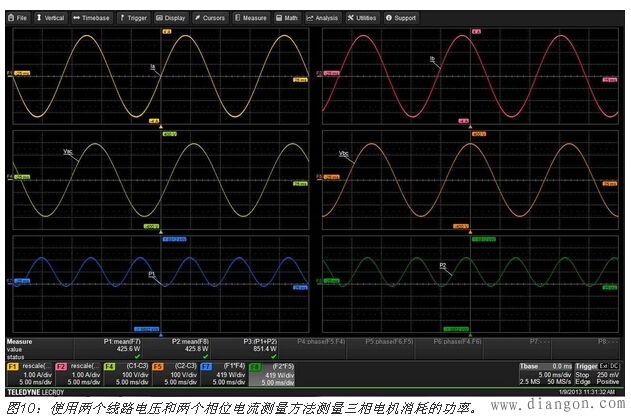
有效功率的两个分量分别是425.6W和425.8W。这两个分量的和——或851.4W(使用P3中参数数学公式计算)——是电机消耗的总有效功率。
波形轨迹平滑
数字示波器是采样型数据仪器。它们利用了著名的采样理论——如果以大于某波形所含最高频率两倍的速率对该波形进行采样,那么就可以在不丢失信息的条件下重建这个波形。这个采样过程的结果是,数字示波器中的波形轨迹由许多数据点组成,如图11所示。
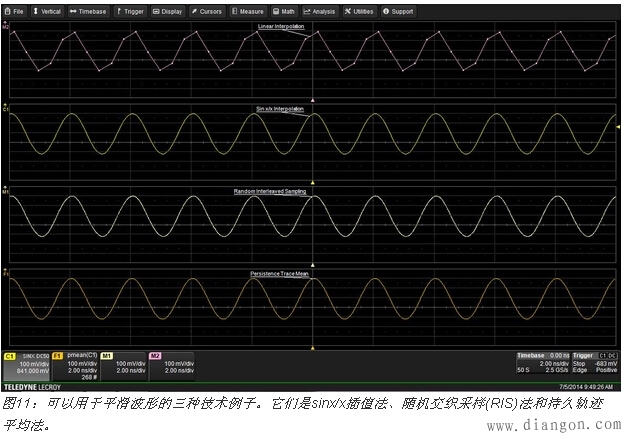
这是一个完全正确的波形,但理解起来有点难度。以某种连续形式观察这些波形的最简单方法是用线将这些点连起来。这种方法被称为线性插值法,图中上方的轨迹显示了一个例子。当屏幕上采样点很少时,这个例子只有50个点,线性插值法经常出现不连续性。一种解决方案是增加采样点数。如果数据是按采样理论进行采样的,那么就可以利用诸如sin(x)/x等插值函数增加采样点数。从上往下数第二条轨迹显示了应用sin(x)/x插值函数的结果,与原始采样数据相比采样点数增加了10倍。
sin(x)/x插值方法的一个缺点是,如果波形有快速边沿,就像脉冲波形中的那样,就可能超过奈奎斯特极限,并且频率分量有可能超过采样频率的一半。在这种情况下,sin(x)/x插值法就无效了,波形会失真。脉冲边沿将出现实际波形中不存在的上冲和下冲现象,即所谓的“吉布斯耳朵”("Gibbs ears.")。
如果波形是重复性的,可以使用随机交织采样——一种等效时间采样方法来增加有效的采样率,并例采样点靠得更近。图11的上方第3条轨迹对此作了展示。如果波形是重复性的,打开显示保留功能将产生仅基于采样值的平滑波形,如图11中下方轨迹所示,其中被称为持久轨迹平均的先进数学工具提供了捕捉持久显示器上每个点均值的能力。
均方根和标准偏差
均方根(rms)和标准偏差(sdev)是密切相关的测量。rms的计算公式是:
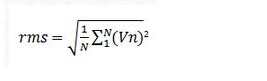
其中N是波形中的点数,Vn是第n个采样点的值。
标准偏差被定义为:
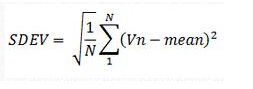
其中N是波形中的点数,Vn是第n个采样点的值,mean是V的平均值。
对于零均值的波形来说,上面两个公式是一致的,rms值和标准偏差相等。当信号均值为非零时,从每个数据点减去均值后的sdev值就是减去均值后样本的rms值。因此sdev是真正的交流rms值(在减去均值后的rms值)。
考虑图12所示3.3V电源输出上的纹波和噪声的测量。
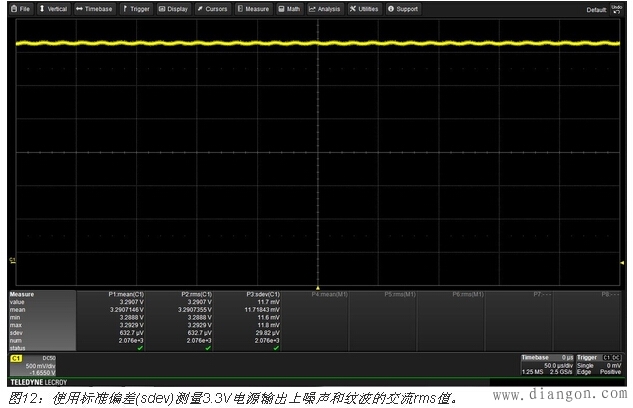
波形均值用参数P1进行读取。这是与纹波和噪声无关的标称直流输出。rms值P2同时包含了均值、纹波和噪声。标准偏差(参数P3中的sdev)仅读取电源输出中的交流分量(噪声和纹波)。要从每个测量点减去均值。因此标准偏差是“交流”rms值。
rms值现在变高了,因为包含了偏移量。知道均值和rms值后就可以计算sdev值了。
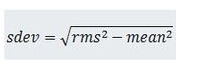
为了计算电源输出上只是噪声和纹波的rms值,你可以选择标准偏差或交流rms。
本文小结
至此你又掌握了另外10个示波器功能的应用,它们可以帮助你扩展这种通用仪器的用途。希望其中一些应用技巧能够帮助到你的日常工作。
