一、开普勒定律
（一）开普勒第一定律
行星绕太阳运行轨道是一个椭圆，太阳位于该椭圆的一个焦点上。
（二）开普勒第二定律
行星围绕太阳运行时，行星与太阳的连线（向径），在相同的时间内扫过相同的面积。
（三）开普勒第三定律
行星绕太阳运行周期的平方，与其轨道长半径的立方成正比。
二、无摄轨道的描述
（一）开普勒轨道根数（Kepler orbital element）
由开普勒定律可知，卫星无摄轨道是一个椭圆。描述椭圆的形状和大小，只需要椭圆长半轴as和偏心率es这两个参数既可。但这样的描述还不能唯一固定卫星轨道平面相对于地球本体的位置。所以，为了固定卫星轨道相对于地球的位置，我们还要引入另外四个个参数。这四个参数加上前面的as和es，一共6个参数，合称为开普勒轨道根数，也叫开普勒轨道参数。
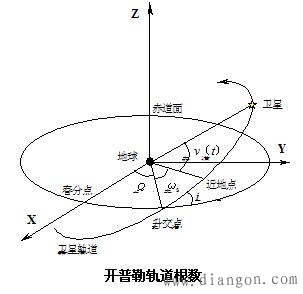
现将6个开普勒轨道根数的常用符号及含义介绍如下。
as——轨道椭圆长半轴（Semi-major Axis）。
es——轨道椭圆偏心率（eccentricity）。
i——轨道面倾角（inclination of orbit）。即卫星轨道平面与赤道面的夹角。
Ω——升交点赤经（right ascension of ascending node）。升交点是指卫星由南向北运行时，其轨道与赤道面的交点。
ωs——近地点角距（argument of perigee）。即轨道平面上，升交点与近地点之间的地心夹角。
τ0——卫星过近地点的时刻（Epoch of perigee passage）。
这6个参数所构成的坐标系统，通常称为轨道坐标系（Elements of Coordinate System），用来描述卫星的运动。它们的大小取决于卫星的发射条件了。
（二）真近点角的计算
真近点角：轨道平面上，卫星与近地点之间的地心角距，可用v（t）表示。为了方便计算，需要引入两个辅助参数M（t）和E（t）。
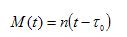
其中n表示卫星运动平均角速度，t表示任意观测历元。
E（t）——偏近点角（eccentric anomaly）。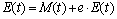
偏近点角E（t）与真近点角v（t）的关系为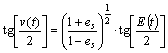
三、卫星坐标的计算
（一）二体问题微分方程
如图所示，根据牛顿万有引力定律，在惯性坐标系中，卫星受到的引力为
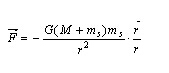
由于卫星质量相对地球为小，可以将式中（M＋ms）忽略为M。由此可得卫星的加速度矢量为
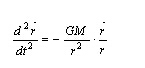
（二）卫星无摄运动瞬时坐标的计算
计算卫星在任意观测历元，相对于地球坐标系的位置，可分三步：首先建立轨道直角坐标系，计算卫星在轨道直角坐标系中的位置；然后计算卫星在天球坐标系下的坐标；最后再将卫星的天球坐标转换为地球坐标系下的坐标。
1．卫星在轨道直角坐标系中的位置
如图3－6所示，取地球质心M为坐标原点，X0轴指向近地点P，Z0轴垂直于轨道平面，Y0轴在轨道面内垂直于X0轴构成右手系。在该坐标系中，卫星ms的坐标为（x0，y0，z0）T。
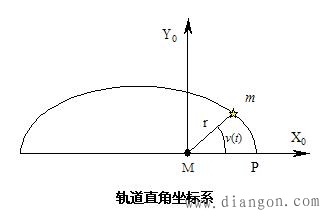
根据图3－6所示，易知
2．卫星在天球坐标系中的位置
由公式（3－18）可以确定卫星在轨道平面上的位置，而卫星在天球坐标系中的位置，还需要轨道参数Ω、ωs和i。天球坐标系与轨道直角坐标系的原点都是地球质心，只是坐标轴指向不相同。为了使两个坐标系相一致，按照坐标系转换的有关理论，需要将坐标轴依次作如下旋转：
●轨道直角坐标系M－X0Y0Z0绕Z0轴旋转角度ωs，使得X0轴指向由升交点。
●旋转后再绕X0轴旋转角度i，使Z0轴与天球坐标系Z轴重合。
●再绕Z0轴旋转角度Ω，使X0轴与天球坐标系X轴重合。
设（X，Y，Z）CS为卫星在天球坐标系中的坐标，则它们的转换关系为
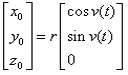
结合上式，可以确定卫星在任意观测历元下，在天球坐标系中的坐标。
3．卫星在地球坐标系中的位置
有了卫星的天球坐标，就可以根据天球坐标系与地球坐标系的关系，进一步计算卫星在地球坐标系中的位置。设（X，Y，Z）TS为卫星在地球坐标系中的坐标。则有
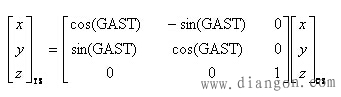
一般说来，最后还需对（x，y，z）TS进行极移改正，将其转化为协议地球坐标系下的坐标（x，y，z）CTS。
归纳起来，卫星无摄运动在轨位置的计算步骤依次为：
——计算平均角速度n；
——计算平近点角M（t）；
——计算偏近点角E（t），利用开普勒方程；
——计算真近点角v（t）；
——计算卫星地心向径r，利用无摄轨道方程；
——计算卫星在轨道直角坐标系中的位置；
——计算卫星在天球坐标系中的位置；
——计算卫星在地球坐标系中的位置；
——对卫星的地球坐标进行极移改正，将其转化为（x，y，z）CTS
至此，卫星在任意观测历元t，在协议地球坐标系下的坐标就计算出来了。顺便指出，通过类似的步骤，也可以推导卫星无摄运行速度分量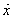
、
、
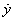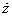在协议地球坐标系中的表达式。