1．戴维南定理
线性含源一端口网络的对外作用可以用一个电压源串联电阻的电路来等效代替。其中电压源的电压等于此一端口网络的开路电压，而电阻等于此一端口网络内部各独立电源置零后所得无独立源一端口网络的等效电阻。这种电路称为戴维南等效电路，如下图示。
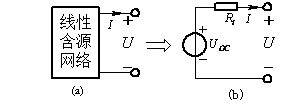
图1 戴维南定理图示
证明：
图2 戴维南定理的证明
响应U是电流源I和网络内部各独立电源激励的线性组合，即
式中
、
是由电路结构和参数决定的系数，它们与各独立源的量值无关；
表示网络内部第k个独立电源（电压源电压或电流源电流），是确定的。因此，
是一确定电压，与电流I无关，用
来表示。于是得到图2(a)所示一端口网络的电压、电流关系：
其中
和
可以按如下方法求得：
(a)令端口所接电流源不作用，即
，如图2(b)，可见
是a,b两端 开路时的电压，记作
(b)令一端口内部各独立电源不作用，即式中
，如图2(c),故
，
,
是当网络内部全部独立电源置零时，从端口处看进去的等效电阻的负值，记作
最终，一端口网络的电压、电流关系可以写成：
上式正是图1(b) 所示戴维南等效电路的电压、电流关系。由此证明了戴维南定理。
2．诺顿定理
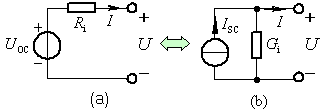
图3 含源电路的等效变换
线性含源一端口网络的对外作用可以用一个电流源并联电导的电路来等效代替，其中电流源的源电流等于此一端口网络的短路电流,而电导等于此一端口网络内部各独立源置零后所得无独立源一端口网络的等效电导。
例题1：计算图4(a)电桥中
分别等于0Ω、0.8Ω、1.6Ω时，该支路的电流和功率。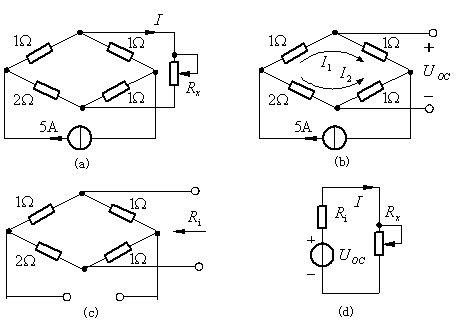 
图4 例题1
解：用戴维南定理化简电路中的不变部分。
(1) 求开路电压
。将
支路断开时，电路如图(b)所示。源电流5A分流成
和
，由分流公式求得
，
故
(1)
(2) 求等效电阻
。将电流源用开路代替，电路如图(c)所示。用串、并联化简得
(2)
(3) 根据(1)、(2)求得戴维南等效电路如图(d)所示。由图(d)得
，
当
分别等于0Ω、0.8Ω、1.6Ω时，由上两式求得该支路的电流和功率分别为0.83A、0.5A、0.36A和0W、0.2W、1.73W。
例题2：图示电路。已知R=8Ω时，I＝1A。求R为何值时I＝0.5A？
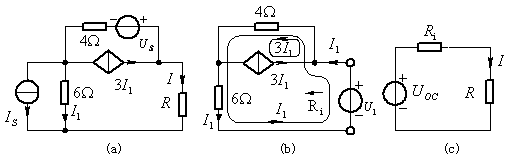
图5 例题2
解：为求出等效电阻，将
和
置零，如图(b)所示。此一端口内部含受控源，不能只用电阻等效化简的方法求
。这时可在端口外加电压源
求端口电流
(也可加电流源求端口电压)，则
，对图(b)列回路电流方程：
戴维南等效电路如图(c)所示。由图(c)及已知条件求得开路电压
再根据题意得
解得
