由于电路是由各种元件以一定的连接方式组成的,每一个元件要遵循它两端的电压电流关系伏安关系,而与结点相连的各条支路电流及回路中各部分电压分别受(KCL)和(KVL)的约束。因此,基尔霍夫定律和元件的伏安关系是分析电路的依据。
分析电路的方法有支路电流法、叠加定理、戴维宁定理等。
在计算电路时选用哪一种方法应视要求解的问题及电路具体结构和参数而定。
(1)支路电流法
支路电流法是以支路电流(电压)为求解对象,直接应用KCL和KVL列出所需方程组,而后解出各支路电流(电压)。它是计算复杂电路最基本的方法。但是,当电路中支路数较多时,联立求解的方程数也就较多,因此计算过程一般较繁琐。所以只有当电路不是特别复杂而且又要求出所有支路电流(或电压)时,才采用支路电流法。
用支路电流法解题的步骤
* 确定支路数b,假定各支路电流的参考方向;
* 应用KCL对结点列方程
对于有n个结点的电路,只能列出(n–1)个独立的KCL方程式。
* 应用KVL列出余下的b–(n–1) 个方程;
* 解方程组,求解出各支路电流。
(2)叠加定理
叠加定理内容:在多个电源共同作用的线性电路中,某一支路的电压(电流)等于每个电源单独作用,在该支路上所产生的电压(电流)的代数和。
注意:计算功率时不能应用叠加定理。在叠加过程中当电压源不作用时应视其短路,而电流源不作用时则应视其开路。但电源内阻仍需保留。
在应用叠加定理计算复杂电路时,由于每个电源单独作用在电路中,因此使得电路较为简单。但当原电路中电源数目较多时,计算就变得很繁琐。所以,只有当电路的结构较为特殊时才采用叠加定理来求解。
叠加定理的重要性不在于用它计算复杂电路,而在于它是分析线性电路的普遍原理。
(3)戴维宁定理
戴维宁定理内容:任意线性有源二端网络N,可以用一个恒压源与电阻串联的支路等效代替。其中恒压源的电动势等于有源二端网络的开路电压,串联电阻等于有源二端网络所有独立源都不作用时由端钮看进去的等效电阻。
戴维宁定理是本章的重点之一,但不是难点。
戴维宁定理把复杂的二端网络用一个恒压源与电阻串联的支路等效代替,从而使电路的分析得到简化。此法特别适用于只需求解复杂电路中某一支路的电流(电压),尤其是这一支路的参数经常发生变化的情况。
运用戴维宁定理应注意:戴维宁定理只适用于线性电路,但对网络外的电路没有任何限制;等效是对外部电路而言的。
(4)电源模型的等效变换
运用电压源与电流源模型的等效变换也可以简化电路的计算。
电源模型等效变换的条件如下图:
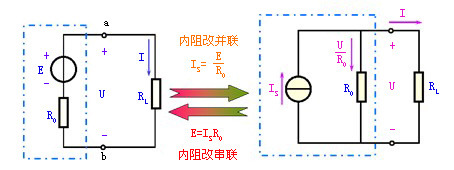
注意:
电压源与电流源模型的等效变换关系仅对外电路而言,至于电源内部则是不相等的。
