电路如图9-1所示,当
![]() ,
,![]() ,
,
可求得
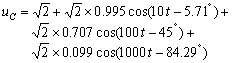
上述结果表明:该电路对![]() 的信号几乎没有衰减和相移,而对
的信号几乎没有衰减和相移,而对![]() 的信号衰减较大
的信号衰减较大
这是由电路频率特性决定的,什么是电路的频率特性?
从第五章可知,对单一频率,响应是激励同频率的正弦量;
而工程中常遇到的是由许多不同次谐波组成的非单一频率激励,由此我们要分析网络在不同频率下的响应与激励间的关系,即网络的频率特性。它是由网络函数表征的。
1.网络函数
若将关心的网络中某一电压(如图9-1中的![]() )或电流作为响应,将电源的源电压(如图9-1中的
)或电流作为响应,将电源的源电压(如图9-1中的![]() )或源电流作为激励,则可定义网络函数:
)或源电流作为激励,则可定义网络函数:
![]() =
=![]() (为频率
(为频率![]() 的函数)
的函数)
式中,![]() 为响应相量,
为响应相量,![]() 为激励相量;网络函数随电源频率的变化而变化。
为激励相量;网络函数随电源频率的变化而变化。
2.网络函数的类型
1)若激励和响应位于同一端口,则网络函数为(输入阻抗)![]() (输入导纳),具有阻抗或导纳量纲,称为策动点阻抗或策动点导纳
(输入导纳),具有阻抗或导纳量纲,称为策动点阻抗或策动点导纳
2)若激励和响应位于不同的端口,则网络函数可以是转移网络函数
| 激励 | 响应 | 转移函数 |
电流 | 电流 | 转移电流比 |
电流 | 电压 | 转移阻抗 |
电压 | 电流 | 转移导纳 |
电压 | 电压 | 转移电压比 |
3.频率特性
将网络函数写成极坐标形式得:![]()
![]() 为网络函数的模,称为网络函数的幅频特性,反映响应与激励有效值之比与频率的关系;
为网络函数的模,称为网络函数的幅频特性,反映响应与激励有效值之比与频率的关系;
![]() 为网络函数的辐角,称为网络函数的相频特性, 反映响应越前于激励 的相位差与频率的关系。
为网络函数的辐角,称为网络函数的相频特性, 反映响应越前于激励 的相位差与频率的关系。
以![]()
![]() 为例,令:
为例,令:![]() (称为RC电路的固有频率)
(称为RC电路的固有频率)
![]() =
=![]() ;
;![]()
取频率的相对值![]() 为0、1、2、…
为0、1、2、…![]() ,计算
,计算![]() 和
和![]() 如下:
如下:
![]() 时
时 ![]()
![]()
![]() 时
时 ![]()
![]()
![]() 时
时 ![]()
![]()
![]()
![]()
![]()
![]() 时
时 ![]()
![]()
可得RC电路的幅频特性曲线如(a)图 相频特性曲线如(b)图

通常将网络函数的模下降到最大值的![]() 时所对应的频率称为截止频率,对应RC低通网络的截止频率为
时所对应的频率称为截止频率,对应RC低通网络的截止频率为![]()
对于低通网络,频率为![]() 这一范围称为低通网络的通带,
这一范围称为低通网络的通带,![]() 频率范围称为阻带。
频率范围称为阻带。
例1 求图示电路的转移电压比H(jω)=![]() 、(
、(![]() 为开路电压),写出其幅频特性和相频特性,指出电压
为开路电压),写出其幅频特性和相频特性,指出电压![]() 的相位随频率变化的范围。
的相位随频率变化的范围。
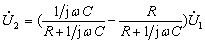
解:由分压公式得
![]()
整理得 ![]()
故有 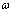
当![]() 从
从![]() 变到
变到![]() 时,
时,![]() 从零变化到
从零变化到![]() 。
。
4.低通,高通,带通,带阻网络
由以上RC串联幅频图可知,当输入电压有效值保持不变的情况下,频率越低,![]() 越大,响应越高;频率越高,
越大,响应越高;频率越高,![]() 越小,响应越低,可以认为此网络允许低频信号通过,而对高频信号产生较大的衰减,称为低通网络。
越小,响应越低,可以认为此网络允许低频信号通过,而对高频信号产生较大的衰减,称为低通网络。
通过选用不同的电路结构和元件输出,可同样实现高通网络,图 9-2 所示的高通网络幅频特性如下。同时给出带通网络和带阻网络幅频特性。
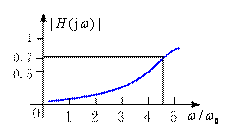
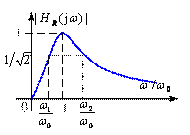
高通网络幅频特性
带通网络幅频特性
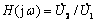
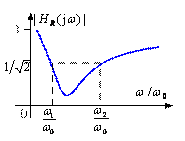
带阻网络幅频特性
例2 求图示电路的网络函数![]() 。
。
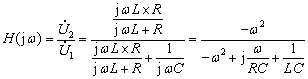
解: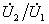
例3 求图示电路的转移电压比H(jω)=![]() ,当R1C1=R2C2时,此网络函数有何特性?
,当R1C1=R2C2时,此网络函数有何特性?
解: 列方程
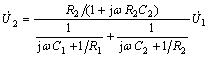
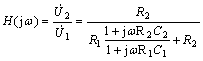
整理得
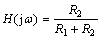
当R1C1=R2C2时,得。此网络函数不受频率变化影响
