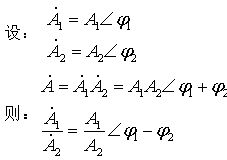一、相量图表示法
设有一旋转矢量,矢量的长度正比于正弦量的幅值Im ,矢量的初始角(即t=0 时矢量的初始位置与横坐标正方向之间的夹角)等于正弦量的初相位ψ,并以正弦量的角频率ω作逆时针匀速旋转。这个旋转矢量任何时刻在纵轴上的投影,正好等于正弦量在同一时刻的瞬时值。
考虑到在正弦交流电路中,各电压和电流均为同一频率。因此在任何瞬时各旋转矢量间的夹角都是不变的,这样即可用一个不旋转的矢量来表示正弦交流电。矢量的长度与正弦交流电的最大值(或有效值)的大小成正比,矢量与横轴正方向的夹角等于正弦交流电的初相位角。
由于表示随时间变化的正弦量的矢量与空间矢量(例如力、电场强度等)有本质区别,因此我们把表示正弦量的矢量称为相量。相量的写法为大写字母的上方加一个点。 I&是电流的有效值相量。如下图。
把数个同频率正弦量的相量画在同一图上,这种表示它们之间大小和相位关系的图形称为相量图。在相量图上,可应用平行四边形法则求任两个相量之和或差。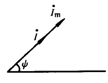
相量
二、相量(复数)表示法
从数学中我们知道,矢量可以用复数表示。那么,表示随时间变化的正弦量的相量,也可以用复数表示,即正弦量可以用复数表示。
其中代数式为
极坐标式为:![]()
三、复数的形式转化与计算
1.代数式与极坐标式的转化
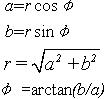
2.计算
1) 复数加、减运算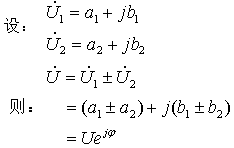
2) 复数乘、除法运算