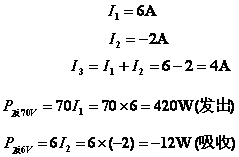运用支路电流法列写电路方程

凡不能用电阻串并联等效变换化简的电路，一般称为复杂电路。在计算复杂电路的各种方法中，支路电流法是最基本的方法之一。它是以各支路电流为未知量，应用基尔霍夫电流定律（KCL）和基尔霍夫电压定律（KVL）分别对结点和回路列写方程组的电路分析方法。

列方程时，必须先在电路图上选定好未知支路电流以及电压或电动势的参考方向。对于有n个结点、b条支路的电路，要求解支路电流，未知量共有b个。只要列出b个独立的电路方程，便可以求解这b个变量。

独立方程的列写：

①从电路的n个结点中任意选择n-1个结点列写KCL方程；

②选择基本回路列写b-(n-1)个KVL方程。

现以图所示的电路为例，来说明支路电流法的应用。在本电路中，支路数b=6，结点数n=4，共需列出6个独立方程。电动势和电流的参考方向如图中所示。

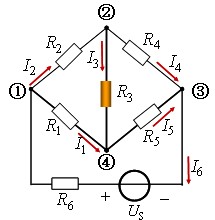
图 支路电流法应用举例

首先，应用基尔霍夫电流定律（KCL）对分别对结点①②③列出

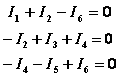(1)

然后，应用基尔霍夫电压定律列出其余b-(n-1)个KVL方程。对网孔列写KVL方程的数目恰好等于b-(n-1)。

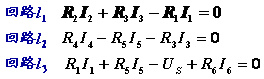(2)

应用基尔霍夫电流定律和电压定律一共可列出(n-1)+b-(n-1)=b个独立方程，所以能解出b个支路电流。

支路电流法的一般步骤：

①标定各支路电流（电压）的参考方向；

②选定(n–1)个结点，列写其KCL方程；

③选定b–(n–1)个独立回路，指定回路绕行方向，结合KVL和支路方程列写；

④求解上述方程，得到b个支路电流；

⑤进一步计算支路电压和进行其它分析。

支路电流法的特点：

支路法列列写的是KCL和KVL方程，所以方程列写方便、直观，但方程数较多，宜于在支路数不多的情况下使用。

例1求各支路电流及各电压源发出的功率。

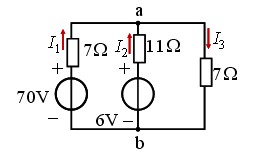
图1

分析：应用支路电流法以I₁、I₂、I₃为求解变量；结点数n=2，支路数b=3，只能列写(n–1)=1个独立KCL方程；余下b–(n–1)=2个方程，需要对网孔列写KVL方程。

解：

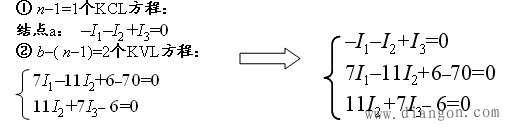
解得