当电路中激励源的频率变化时，电路中的感抗、容抗将跟随频率变化，从而导致电路的工作状态亦跟随频率变化。因此，分析研究电路和系统的频率特性就显得格外重要。
频率特性：电路和系统的工作状态跟随频率而变化的现象，称为电路和系统的频率特性，又称频率响应。
1、 网络函数的定义
在线性正弦稳态网络中，当只有一个独立激励源作用时，网络中某一处的响应（电压或电流）与网络输入之比，称为该响应的网络函数。
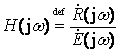
2、网络函数H(jω)的物理意义
① 驱动点函数：在如图1(a)所示电路中，根据网络函数的定义，得到
激励是电流源，响应是电压：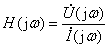
→ 策动点阻抗
激励是电压源，响应是电流：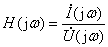
→ 策动点导纳
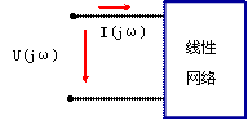(a) |
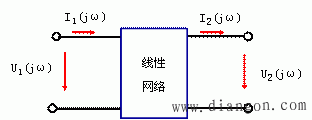(b) |
② 转移函数（传递函数）：在如图1(b)所示电路中，由于激励可以为电流或电压，响应可以为电流为电压，根据网络函数的定义，得到
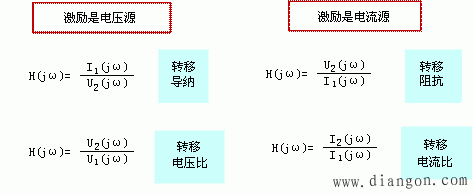
H(jw) 与网络的结构、参数值有关，与输入、输出变量的类型以及端口对的相互位置有关，与输入、输出幅值无关。因此网络函数是网络性质的一种体现。网络函数可以用相量法中任一分析求解方法获得。H(jw)是一个复数，它的频率特性分为两部分：
幅频特性：模与频率的关系 →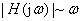
相频特性：幅角与频率的关系 →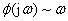
注意
- 以网络函数中jω的最高次方的次数定义网络函数的阶数；
- 由网络函数能求得网络在任意正弦输入时的端口正弦响应，即有
→