在实际电路中常会含多个电阻元件。这些电阻元件根据不同需要按一定方式连接起来，便于在各种不同情况下获得不同的电压、电流及功率。电阻的连接方式有串联、并联、混联三种。
一、电阻的串联<?XML:NAMESPACE PREFIX = O />
电路中有两个或更多个电阻顺序相联，称为电阻的串联。电阻串联时，通过各电阻的电流是同一个电流。
如图所示n个电阻串联时，根据KVL有
<?XML:NAMESPACE PREFIX = V />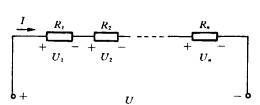
其中 
称为这些串联电阻的等效电阻。它与这些串联电阻所起的作用是一样的。
可以看出，n个串联电阻吸收的总功率等于它们的等效电阻
吸收的功率。
必大于任一个串联中的电阻。
电阻串联时，各电阻上的电压为
此式称为电压分配公式，它表明各个串联电阻的电压与其电阻值成正比；或者说总电压按各个串联电阻的电阻值进行分配。
电阻串联电路应用广泛，常用来降压，调节电流、分压等。
二、电阻的并联
电阻的并联：电路中两个或更多个电阻都连接在两个公共的结点间。称为电阻的并联，电阻并联时，各并联电阻两端承受同一电压。
如图所示中n个电阻并联时，根据KVL有
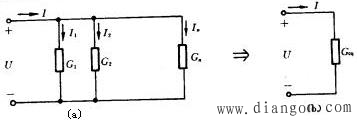
其中 
称为这些并联电阻的等效电导。所以我们可以用一个电导等于
的电阻来代替这n个并联电阻，如图（b）所示。
可以看出，n个并联电阻的总功率等于它们的等效电阻吸收的功率。由于等效电阻
，而各个并联电阻
，故有
这样有
，即等效电阻总小于任意一个并联中的电阻。
电阻并联时，各电阻中的电流为
上式称为电流的分配公式，它表明各个并联电阻中的电流与它们各自的电导成正比；或者说总电流按各个并联电阻的电导进行分配。
例如对于两个电阻的并联如图所示，根据上述结论，有
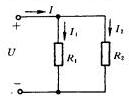
即等效电阻
为
两分电流的分配关系为
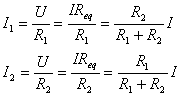
我们在此特别提出两电阻的分流关系是因为我们在后续电路分析中经常要用到这个关系式。
三、电阻的混联
既有电阻串联又有电阻并联的电路叫电阻混联电路。这种电路在实际工作中应用广泛、形式多种多样。如图所示。
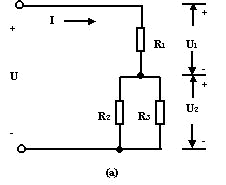
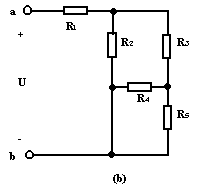
分析混联电路，首先要弄清电路中各电阻的连接关系。
通过同一电流的各电阻一定是串联关系；
连接在共同两点之间的各支路一定是并联关系；
通常连接导线的电阻可忽略不计，因此电位相等的连接线可收缩为一点，反之，一个接点可拉长为一根导线。
根据以上三点，可将不易看清串并联关系的电路，改画整理成便于识别的电路，但连接关系不能变更。如图（b），可将b点缩为一点即可看出
，因而可得等效电阻
，然后运用串、并联电路特点和欧姆定律进行分析和计算。
四、电阻电路的等效变换
对于一个较为简单的线形电阻电路，如能通过电阻串联和并联的等效变换来化简电路，就可很方便地求出未知量。
例：求图所示电路中的a、b两点间的等效电阻
。
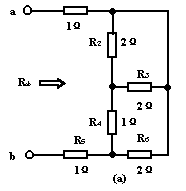
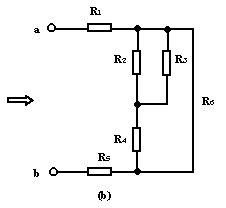
解：图（a）中
与
并联，电路可简化为图（b）所示。
根据串、并联的有关公式并代入数值，可得
