74LS138是一种集成的3-8线译码器芯片。它的逻辑电路如图1所示。
 |
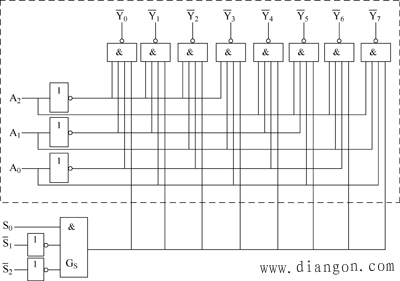| 图1 3.8线译码器的电路图 |
从图1可以看出，74LS138电路除了双点画线框内的译码电路外，还包含了由GS门组成的控制电路部分。
74LS138有3个附加的控制端S0、S1、和S2。当S0=1、
时，GS输出为高电平（1），译码器处于正常工作状态；否则，译码器被禁止，所有的输出被锁定在高电平。这3个控制端又称“片选”输入端，利用片选的作用可以将多片连接起来以扩展译码器的功能。
表1 74LS138译码器的逻辑功能表
| 输入 | 输出 | |||||||||||
| S0 |  + |
A2 | A1 | A0 | Y7 | Y6 | Y5 | Y4 | Y3 | Y2 | Y1 | Y0 |
| 0 | × | × | × | × | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| × | 1 | × | × | × | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | 1 |
| 1 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | 1 | 1 |
| 1 | 0 | 1 | 0 | 0 | 1 | 1 | 1 | 0 | 1 | 1 | 1 | 1 |
| 1 | 0 | 1 | 0 | 1 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 1 |
| 1 | 0 | 1 | 1 | 0 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 1 |
| 1 | 0 | 1 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
从表1可以看出，输入变量的每一组状态对应着一个输出端的低电平0信号，因此当输出端输出低电平0时，认为该端有信号输出，称为输出端为低电平有效，相应地输出变量的字母上面画一短线。只有当S0=1、时，译码器才处于工作状态，否则译码器不工作，输出端全部为高电平1。因此译码器工作时，，因此称控制端、也为低电平有效，用字母上画一短线表示。图2所示为5-6-4的逻辑图形符号，输入、输出端靠近方框外的小圆圈表示低电平有效。
 |
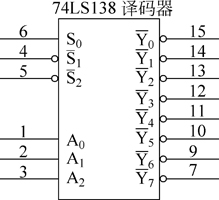| 图2 74LS138逻辑符号 |
例1：试用两片74LS138组成4-16线译码器，将输入的4位二进制代码A3A2A1A0译成16个独立的低电平信号
～
。
解：由图2可知，一片74LS138芯片只有3个代码输入端A2、A1、A0，想要对4位代码进行译码，必须用控制端来补充作为第4个代码输入端A3。
由74LS138的逻辑功能表1可知，控制端S0=1、时译码器才能工作，否则译码器不工作。因此，可以用第4个代码输入端A3作为高位端，通过该端的状态分别控制两片74LS138芯片的工作状态。逻辑电路如图3所示。
 |
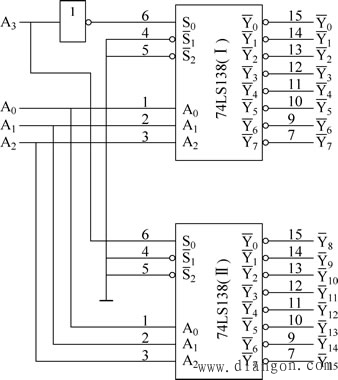| 图3 例1的逻辑电路图 |
当然，连线的方式不止这一种，请读者自行分析。
由表1可知，当S0=1、时，译码器处于工作状态，而且若将A2、A1、A0作为3个逻辑输入变量，则8个输出端给出的就是这3个输入变量的全部最小项，即
 |
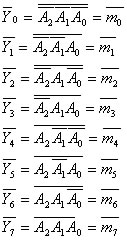(1) |
利用附加的门电路将这些最小项适当地组合起来，可以产生任何形式的三变量组合逻辑函数。
同理，由于n位二进制译码器的输出给出了n个变量的全部最小项，因此用n变量的二进制译码器可以获得任意形式的输入变量不大于n的组合逻辑函数。
例2：试用3-8线译码器74LS138和门电路实现下列组合逻辑函数。
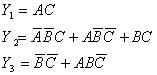
首先将给定的组合逻辑函数式化成最小项之和的形式，即
 |
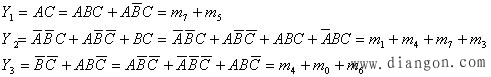(2) |
由图1和式（1）可知，只要令74LS138的输入A2=A，A1=B，A0=C，则它的输出～
就对应着式中的
～
。
所以将式（2）化成最小项非的形式，即
 |
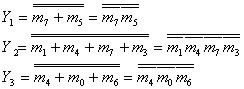(3) |
上式表明，只要在74LS138的输出端附加3个与非门就可以得到所要求的逻辑函数。电路的解法如图图4所示。
 |
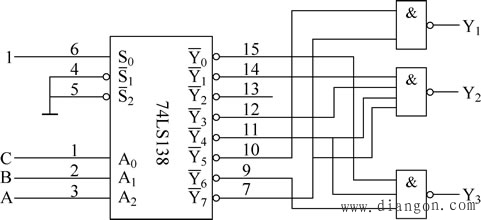| 图4 例3的电路图 |