相位差法属回波法,常用于大位移量(距离)的测量之中。相位差检测的载体是光波或电磁波。
由光的波动性可知,光波是横波,它在空间传播,其振动方程为:
a=ACOS(Ωt+![]() ) (1)
) (1)
式中,A为光波的振幅;Ω为光波的角频率;![]() 为光波初相位。
为光波初相位。
要把光应用于测位移,必须对光进行调制。
光的调制,就是利用某种人为的信息对光的发射进行控制的过程。通过控制使发射光带上的可以利用的人为信息传输出去。一般称人为信息为调制信号。
设调制信号遵循正弦函数变化,它能使光的振幅A也发生正弦函数变化,亦即
A=A0+△Asin ωt (2)
式中,A0为未调制的光波振幅;△A为引起振幅变化的最大值,ω为信号的振荡角频率,且ω<<Ω。将式2代入式1,并令![]() =0,得
=0,得
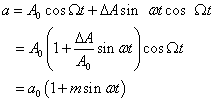 (3)
(3)
式中:
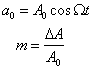 (4)
(4)
从物理光学中可知,光的强度与其振幅的平方成正比,且又表现为原子振荡周期内的平均值,故用1,表示式4的发光强度,则
![]()
式中,K为比例系数。显然,J所表示的光源发光强度是一个定值。由此可见,式3的a0是一个定值。
一般说来,要把调制信号加在发射的光中,必须通过一种称调制器的器件方能完成。图1表示光波经过调制器后光波被调制所形成的图像。
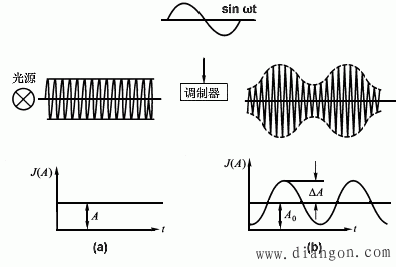
图1 光波经调制所彤成的图像
图1(b)虚线(包络线)表示在调制信号作用下光波的强度发生了遵循正弦规律的缓慢变化,其幅度的大小表示了光强.J(A)明暗的有规律变化。式3中m称为调制度。由于m的存在,光波强度的明暗变化遵循调制信号的特征,其频率与调制信号频率![]() 相同(称
相同(称![]() 为调制频率)。那么原来无法利用的光变为光强度的明暗(或光波振幅)遵循调制信号频率
为调制频率)。那么原来无法利用的光变为光强度的明暗(或光波振幅)遵循调制信号频率![]() 变化的光波,就是调制光波。在这里角频率为Ω的光波运载着频率为
变化的光波,就是调制光波。在这里角频率为Ω的光波运载着频率为![]() 的信号传输出去,故称光源发出的光波为载波。
的信号传输出去,故称光源发出的光波为载波。
相位差法测位移所需要的光波是利用一种遵循正弦规律的信号通过某种方式(如采用调制器)把连续光波强度转变为明暗(或称波的振幅大小)连续变化的调制光波。利用这种明暗变化的调制光波就能达到测位移的目的。
波在传播过程中所产生的相位移![]() 与传播的路程х有密切的关系。在这里,用
与传播的路程х有密切的关系。在这里,用![]() 表示相位移,则根据波动方程,有关系式
表示相位移,则根据波动方程,有关系式
![]() (5)
(5)
式中,ω为波的角频率,ω=2π![]() ,
,![]() 是波的振荡频率;v为波的速度(即电磁波的速度C)。设波传播经过路程χ所需时间为t,则t=
是波的振荡频率;v为波的速度(即电磁波的速度C)。设波传播经过路程χ所需时间为t,则t=![]() ,故上式又可表示为
,故上式又可表示为
![]() =2π
=2π![]() ·t (6)
·t (6)
由此可知
![]() (7)
(7)
设测距仪从A点发射调制光波,到达B点反射器又反射回测距仪,经历了2D的路程,则有关系式
![]() (8)
(8)
式8表明,只要通过测定调制光波经2D的相位移![]() ,便可间接测定t2D。,获得所需的距离D来。相位差法测距因此而得名。
,便可间接测定t2D。,获得所需的距离D来。相位差法测距因此而得名。
为了进一步说明相位差法测距原理,我们把光的发射与接收过程画成波形如图2的情形,即把往返所测距离D的调制光波展在2D上。从图中可以看到,调制光波经2D有N个整周期的波和不足一个周期的波,故调制光波经2D 产生的相位移![]() 可以用下式表示,即
可以用下式表示,即
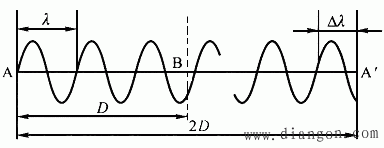
图2 光的发射与接收过程
![]() =N·2π+△N·2π (9)
=N·2π+△N·2π (9)
式中,N为调制光波的整波数,△N为调制光波最后部分不足整波的尾波数
把式9代入式8中,则得
![]() (10)
(10)
由于λ=![]() ,令μ=
,令μ=![]() ,则上式为
,则上式为
D=u(N+△N) (11)
式中,λ为调制波长,μ为测尺长,简称测尺,即
![]() (12)
(12)
显然在光速C已知的情况下,μ便决定于调制频率![]() ,故又称
,故又称![]() 为测尺频率。
为测尺频率。
由于μ长度一定,那么对于某一距离D来说,N及△N也是一定的。从式11可见,相位法测距就宛如我们拿着一把一定长度μ,的测尺,一尺一尺地丈量距离一样,只要测得整尺数N及尾尺数△N,便可以根据式11计算出所测的距离D来。
图3为相位差法测距仪的基本结构方框图。从图可见,相位差法测距仪结构包括光源、调制器、光的接收装置、测相装置以及高频振荡器、电源等电子电路。
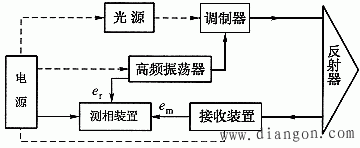
图3 相位差法测距仪结构框图
光源 这是测距仪发射载波光束必不可少的器件。
调制器这种装置在外加信号(调制信号)的作用下,对载波进行调制,从而发射出调制光波。能产生调制信号的装置在电子电路中称为高频振荡器,在测距中一般称为主机振荡器。
反射器 它是测距仪精密测距不可缺少的独立部件,具有最大限度反射光波的作用。
接收装置 在测距仪中能够把反射器反射回来的调制光波接收下来,并且及时转换为具有返回光信号特征的电信号——测距信号em。
测相装置 该装置用于测定光波经2D的相位变化量。由于高频振荡器不仅给调制器提供调制信号,同时又给测相装置提供参考信号er。测相装置又有来自接收装置的测距信号em。在测相装置中比较er、em二信号的相位差,从而获得光经2D的相位移![]() 。由于er、em的频率都由高频振荡器所决定,故er、em都属于同频率信号。显然,在测相装置中,把调制光波经2D相位移
。由于er、em的频率都由高频振荡器所决定,故er、em都属于同频率信号。显然,在测相装置中,把调制光波经2D相位移![]() 的测定转化为二同频信号的相位差比较,从而测得
的测定转化为二同频信号的相位差比较,从而测得![]() 。
。
电源 测距仪正常工作的能源设备。
相位差法测量是目前大位移(距离)测量用得较多的一种方法。根据波的种类,可分为激光测距、无线电波测距等。
