1.二进制异步加计数器的原理
原理分析:假设各触发器均处于0态,根据电路结构特点以及D触发器工作特性,不难得到其状态图和时序图,它们分别如图8.4.2和图8.4.3所示。其中虚线是考虑触发器的传输延迟时间tpd后的波形。
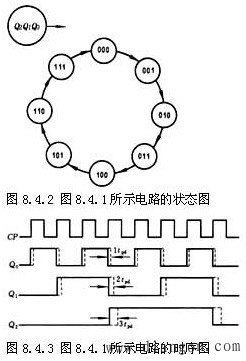
由状态图可以清楚地看到,从初始状态000(由清零脉冲所置)开始,每输入一个计数脉冲,计数器的状态按二进制递增(加1),输入第8个计数脉冲后,计数器又回到000状态。因此它是23进制加计数器,也称模八(M=8)加计数器。
从时序图可以清楚地看到Q0,Q1,Q2的周期分别是计数脉冲(CP)周期的2倍,4倍、8倍,也就是说Q0,Q1,Q2,分别对CP波形进行了二分频,四分频,八分频,因而计数器也可作为分频器。
需要说明的是,由图8.4.3中的虚线波形可知,在考虑各触发器的传输延迟时间tpd时,对于一个n 位的二进制异步计数器来说,从一个计数脉冲(设为上升沿起作用)到来,到n 个触发器都翻转稳定,需要经历的最长时间是ntpd ,为保证计数器的状态能正确反应计数脉冲的个数,下一个计数脉冲(上升沿)必须在ntpd 后到来,因此计数脉冲的最小周期Tmin=ntpd 。
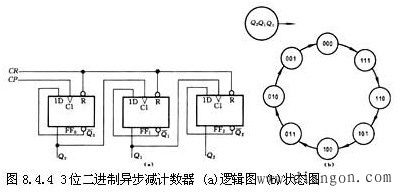
2.二进制异步减计数器的原理
原理分析:图8.4.4是3位二进制异步减计数器的逻辑图和状态图。从初态000开始,在第一个计数脉冲作用后,触发器FF0由0翻转为1(Q0的借位信号),此上升沿使FF1也由0翻转为1(Q1的借位信号),这个上升沿又使FF2 由0翻转为1,即计数器由000变成了111状态。在这一过程中,Q0向Q1进行了借位,Q1向Q2进行了借位。此后,每输入1个计数脉冲,计数器的状态按二进制递减(减1)。输入第8个计数脉冲后,计数器又回到000状态,完成一次循环。因此,该计数器是23进制(模8)异步减计数器,它同样具有分频作用。
3.二进制同步加计数器,同步减计数器的原理
二进制同步加计数器的原理分析:图8.4.5是用JK触发器(但已令J=K)组成的4位二进制(M=16)同步加计数器。
由图可见,各位触发器的时钟脉冲输入端接同一计数脉冲CP ,各触发器的驱动方程分别为J0=K0=1,J1=K1=Q0、J2=K2=Q0Q1、 J3=K3=Q0Q1Q2 。
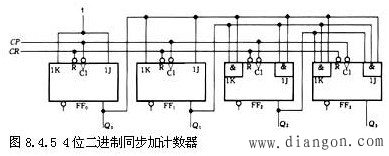
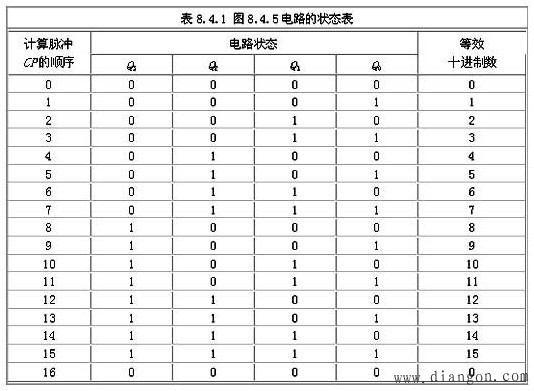
根据同步时序电路的分析方法,可得到该电路的状态表,如表8.4.1所示。设从初态0000开始,因为J0=K0=1,所以每输入一个计数脉冲CP,最低位触发FF0就翻转一次,其他位的触发器FFi仅在 Ji=Ki=Qi-1Qi-2……Q0=1的条件下,在CP 下降沿到来时才翻转。
二进制同步减计数器的原理分析:同步计数器的电路结构较异步计数器复杂,需要增加一些输入控制电路,因而其工作速度受这些控制电路的传输延迟时间的限制。如果将图8.4.5电路中触发器FF1、FF2和FF3的驱动信号分别改为如下所示,即可构成4位二进制同步减计数器.

4.二进制同步可逆计数器的原理
原理分析:4位二进制同步可逆计数器如图8.4.7所示,它是在前面介绍的4位二进制同步加和减计数器的基础上,增加一控制电路构成的。由图可知,各触发器的驱动方程分别为
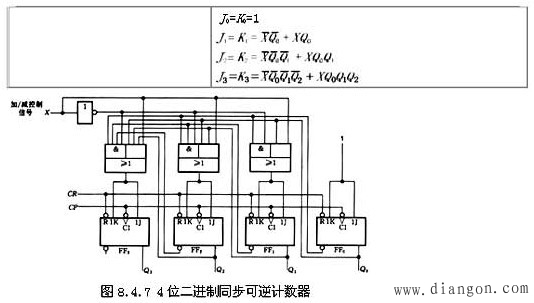
当加/减控制信号X=1时,FF1-FF3中的各J、K 端分别与低位各触发器的Q 端接通,进行加计数;当X=0时,各J、K 端分别与低位各触发器的Q 端接通,进行减计数,实现了可逆计数器的功能。
