系统的特性通常用它的数学模型来描述,也是进行系统设计计算的基础。这里主要讨论系统的线性数学模型,用它的传递函数和频率特性来表示。在介绍各种补偿方法之前,先抓住伺服系统的稳态精度与过渡过程品质,简单地讨论它们与系统特性的关系,以利于对各种补偿方法和补偿装置的功效的理解。
1.系统特性与稳态精度的关系
系统的稳态精度是用稳态误差的数值来衡量的。伺服系统的稳态误差,不仅与系统的特性有关,而且与输入信号的类型有关。常用来分析伺服系统稳态误差的典型输入信号有四种,即阶跃信号、斜坡信号(或称等速信号)、抛物线信号(或称等加速信号)和正弦信号(或称谐波信号)。
设伺服系统的开环传递函数为

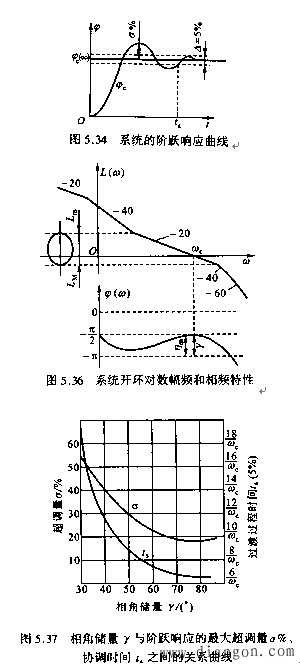
以上简单的分析表明:影响系统稳态精度的主要是系统的低频段特性,具体讲,就看系统的开环增益的大小和串联积分环节的多少。系统开环幅频特性中频段的位置与形状,直接关系到系统的过渡过程品质,它们都与系统的开环增益和开环零、极点分布的状况有关。这也是我们讨论以下各种补偿作用的主要依据。
