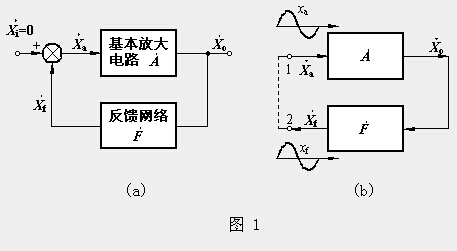
图1a为正反馈放大电路方框图。由图可知, ![]() ,
, ![]() 为反馈信号,它是信号
为反馈信号,它是信号 ![]() 经过基本放大电路和反馈网络所构成的环路传输后得到的,如果
经过基本放大电路和反馈网络所构成的环路传输后得到的,如果 ![]() 与
与 ![]() 在大小和相位上都一致,那么,就可以使输入信号
在大小和相位上都一致,那么,就可以使输入信号 ![]() ,将
,将 ![]() 直接输入
直接输入 ![]() 端,形成如图1b所示的闭环系统,因此,从结构上看,正弦波振荡电路就是一个没有输入信号的带选频网络的正反馈放大电路。
端,形成如图1b所示的闭环系统,因此,从结构上看,正弦波振荡电路就是一个没有输入信号的带选频网络的正反馈放大电路。
振荡条件
|
由于
或 上式中设
式(2)称为振幅平衡条件,而式(3)则称为相位平衡条件,这是正弦波振荡电路产生持续振荡的两个条件。值得注意的是,从负反馈放大电路的自激条件( |
振荡频率
|
振荡电路的振荡频率f0是由式(3)的相位平衡条件决定的。一个正弦波振荡电路只在一个频率下满足相位平衡条件,这个频率就是f0,这就要求在 |
起振与稳幅
|
前面所讲的振幅平衡条件,是指振荡电路中已进入稳态振荡而言的。 欲使振荡电路能自行建立振荡,就必须满足 由于正弦波振荡电路中的放大器件是工作在线性区(RC振荡电路)或接近线性区(LC振荡电路),因此在分析中,可以近似按线性电路来处理。 |
