电路动态响应的分解

零输入响应与零状态响应

我们已经知道，动态电路中的响应不仅与外加激励有关，还与电路的初始储能情况即电路的状态有关。在无外加激励时，仅由电路的非零初始状态也能引起响应。因此，电路的响应可以分解为零输入和零状态成分。
零输入响应(ZIR)：y_x电路的输入为零，仅由初始状态引起的响应。
零状态响应(ZSR)：y_f电路的初始状态为零，仅由外加输入引起的响应。
由电路的状态和输入同时引起的响应称为完全响应。
(1)状态量uc和i_L的零输入和零状态响应
对于电容电压和电感电流变量来说，因为它们的初始值y(0)就代表电路的初始状态，因此，由动态方程解的第一种形式，可知它们零输入响应为

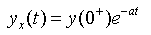
零状态响应为

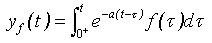
因此，uc和i_L的零输入响应由它们的初始值确定，与输入无关；其零状态响应与其初始值无关，仅由外加输入确定。
(2)一般变量的零输入和零状态响应
非状态变量的初始值y(0)并不代表电路的初始状态，它不仅与电路的初始状态有关，还与电路的输入在t=0+时刻的取值有关。一般变量的零输入和零状态分量的求法是：
零状态：令i_L(0+)=0，uc(0+)=0，保留输入，确定y_f(0+)；
零输入：令输入为零，保留i_L(0+)和uc(0+)，确定y_x(0+)。

由一阶动态方程解的第二种形式

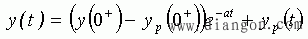
当常数a>0时，响应的第一项随着时间延长衰减而趋于零，称为电路的暂态响应 y_t(t)。响应的第二项y_p(t)取决于电路外加输入，若输入不随时间衰减（如直流，正弦信号，一般周期信号等），则y_p(t)也是同样形式的稳定信号，此时称y_s(t)=y_p(t)为稳态响应。因此，电路的完全响应由可以分解为
y(t) = y_t(t) + y_s(t)

图示电路中，已知uc(0^-)=Uo,且u_s=Us>Uo, 在t=0时接入，
求uc(t)及其各个响应分量。
解由前面讨论，uc的方程为

设完全响应分解为

其中零输入响应为

我们知道电容电压在换路时不会突变


由动态响应的第一种解法，可计算出零状态响应

完全响应


将完全响应重新写成

可以看出，暂态响应为

稳态响应为