并项法是利用公式
，将函数的两个与项合并为一个与项。 例 化简函数
解：
=
=
例 化简函数
解：
=
=
=
2、吸收法
利用公式A+AB=A，吸收多余项。
例 化简函数
解：
3、消去法
利用公式
，消去某项的多余因子。 例 化简函数
解：
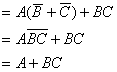
例 化简函数
解：
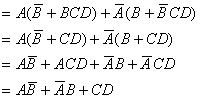
4、消项法
利用多余项定理
，消去多余项BC。 例 化简函数
解：
例 化简函数
解：
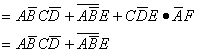
5、配项法
利用公式A+A=A,
,A·A=A，
等，给某逻辑函数表达式增加适当的项，进而消去原来函数的某些项，以达到化简的目的。 例 化简函数
解：
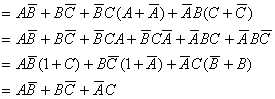
6、综合举例
实际化简复杂逻辑函数时，往往要同时用到各种定律和公式，要进行综合分析，灵活、交替地运用上述方法，才能得到最后的化简结果。
多练习，熟能生巧。
例 化简函数
Y
