1、、基尔霍夫定律的复频域形式
KVL KCL
复频域形式
![]()
2、元件伏安关系的运算形式
将电路元件用相对应的运算关系表示,就得到了元件的运算电路模型。如图34-1所示。在运算电路图中,动态电路的非零独立初始条件与之响应的电源等效,它们称为附加电源,要特别注意它们的参考方向。
R![]()
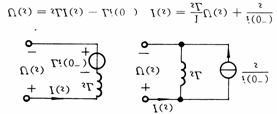
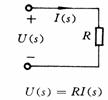
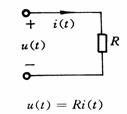
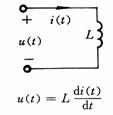
L![]()
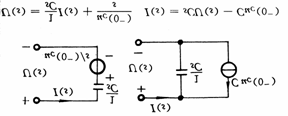
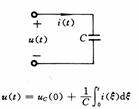
C![]()
<?xml:namespace prefix = o />
M
![]()
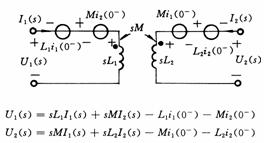
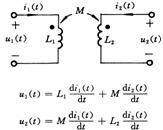
3、应用拉普拉斯变换分析动态电路
应用拉普拉斯变换分析动态电路的关键在于正确地画出复频域等效电路。在零状态下,因电路基本定律的复频域形式以及复频域等效电路,在形式上与相量形式的基本定律以及相量电路相同,所以,对此种情况下的电路复频域分析(运算法)与相量法类似。在非零状态下,只要把电路中的非零独立初始条件考虑成附加电源,电路的运算形式仍和相量形式相似。因此相量法中各种计算方法和定理形式完全可以移用于运算法。具体步骤如下:
1)根据换路前![]() 的电路,求出电感电流
的电路,求出电感电流![]() 和电容电压
和电容电压![]() 在
在![]() 时刻的值,即
时刻的值,即![]() 。
。
2)将激励函数进行拉氏正变换。
3)将换路后![]() 的时域电路变换为复频域电路。
的时域电路变换为复频域电路。
4)应用结点法、网孔法、回路法、以及电路的各种等效变换和电路定理,对运算电路建立方程,并求解得到响应的象函数。
5)利用拉氏反变换,求的得时域响应,并画出波形。
