1、电流:电荷(带电粒子)的宏观定向运动即形成电流。
电流形成的条件:(1)可以自由运动的电荷——自由电荷。(2)电场的存在(超导例外)。
电流的正方向:规定为正电荷运动的方向。
电荷(带电粒子):又称为载流子,可正、可负。
2、电流强度:单位时间内通过导体任一截面的电量。表示式为:
![]()
单位:安培,符号为:A
电流强度只能粗略地描述电荷在导体内的整体流动情况,不能细致描述导体内各点的电荷流动(电流)情况,为了细致描述导体内各点的电荷流动(电流)情况,我们引入电流密度矢量的概念。
3、电流密度
定义:垂直通过导体单位面积的电流强度,用符号j来表示。
方向:正电荷运动的方向。
意义:单位时间内垂直通过导体单位面积的电量,它是空间坐标的矢量点函数。
电流线:电流密度矢量线称为电流线;
电流场:电流密度的分布形成电流矢量场;
电流密度与电流强度的关系:
按定义:![]()
①dS面与j垂直(垂直通过dS的电流):dI=jdS
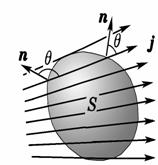
②dS面与j有夹角θ(非垂直通过dS的电流):dI=jdScosθ=![]()
③通过任意曲面S的电流:![]()
二、电流的连续性方程
j对任意闭合曲面的通量的物理意义是:单位时间内流出S面的电量。从面内的电荷来考虑,单位时间内电荷的减少量为:![]() ,显然以上二者是相等的,即
,显然以上二者是相等的,即
![]()
此式称为电流的连续性方程,电流的连续性方程是电荷守恒定律在此的具体表现。
三、稳恒电流和电场
1、稳恒电流:各点的电流密度都不随时间变化的电流。
电流的稳恒条件:空间各点电荷分布必不随时间变化;即任意闭合曲面内的电量没有变化,故得:
![]()
此式称为电流的稳恒条件。
物理意义为:
单位时间内流进闭合面S的电量等于流出的电量;或穿进S的电流线的根数等于穿出S的电流线的根数,即电流线在电路中任何地方不能中断;
直流电路的组成条件:电流线在电路中不中断,即直流电路必须是闭合的。
2、稳恒电场:
稳恒电路中的电场称为稳恒电场。其与静电场的异同为:起源不同,一个来自流动的电荷,一个来自静止电荷;性质相同,均满足静电场方程。
