一、概述
（一） 系统性误差与随机性误差
按照加工误差的性质，加工误差可分为系统性误差和随机性误差。
1. 系统性误差 系统性误差可分为常值性系统误差和变值性系统误差两种。在顺序加工一批工件时，加工误差的大小和方向皆不变，此误差称为常值性系统误差，例如原理误差，定尺寸刀具的制造误差等。在顺序加工一批工件时，按一定规律变化的加工误差，称为变值性系统误差，例如 在刀具处于正常磨损阶段由于刀具尺寸磨损所引起的误差。
2. 随机性误差 在顺序加工一批工件时，加工误差的大小和方向都是随机变化的，这类误差称为随机性误差；例如，由于加工余量不均匀和材料硬度不均匀等原因引起的加工误差、工件的装夹误差、测量误差以及由于内应力重新分布引起的变形误差等均属随机性误差。
(二) 机械制造中常见的误差分布规律
1. 正态分布
2. 平顶分布
3. 双峰分布
4. 偏态分布
(三) 正态分布
1． 正态分布规律
2． 机械加工中，工件的尺寸误差是由很多相互独立的随机性误差综合作用的结果，如果其中没有一个随机性误差是起决定作用，则加工后工件的尺寸将呈正态分布， 值取决于机床调整尺寸和常值性系统误差， 只影响曲线的位置，不影响曲线的形状； 值取决于随机性误差和变值性系统误差， 只影响曲线的形状，不影响曲线的位置； 愈小，尺寸分布范围就愈小，加工精度就愈高。
3． 标准正态分布的正态分布称为标准正态分布，其概率密度
4． 计算工件尺寸落在某一尺寸区间内的概率
工件加工尺寸落在区间（
）内的概率为图4 -47所示阴影部分的面积F（
）
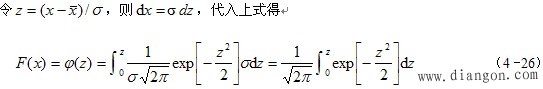
），这就是工程上经常用到的“±3 原则”，或称“6 原则”。二、加工误差的统计分析——工艺过程的分布图分析方法
（一） 工艺过程的稳定性
工艺过程的稳定性是指工艺过程在时间历程上保持工件均值 和标准差 值稳定的性能。如果工艺过程中工件加工尺寸的瞬时分布中心（或工件尺寸均值 ）和标准差 基本保持不变或变化不大，就认为工艺过程是稳定的
（二）工艺过程分布图分析方法
通过工艺过程分布图分析，可以确定工艺系统的加工能力系数、机床调整精度系数和加工工件的合格率，并能分析产生废品的原因。
三、加工误差的统计分析——工艺过程的点图分析方法
（一）点图的基本形式
点图分析法所采用的样本是顺序小样本，即每隔一定时间抽取样本容量n为5~10的小样本，并 计算小样本的算术平均值 和极差R
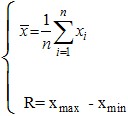
点图的种类很多，目前用得最多的是 图，图所示。 图的横坐标是按时间先后采集的小样本的组序号，纵坐标各为小样本的均值 和极差R。在 点图上有五根控制线， 是样本平均值的均值线，ES、EI分别是加工工件公差带的上、下限，UCL、LCL分别是样本均值 的上、下控制限；在R点图上有三根控制线， 是样本极差R的均值线，UCL、LCL分别是样本极差的上、下控制限。
值点图是控制分布中心变化的，R值点图是控制分散范围变化的，综观这两个点图的变化趋势，才能对工艺过程的稳定性作出评价。