相量法的基础_正弦量的相量表示_相量图_相量法的应用

　　正弦稳态线性电路中，和各支路的电压和电流响应与激励源是同频率的正弦量，因此应用基尔霍夫定理分析正弦电路将遇到正弦量的相减运算和积分、微分运算，在时域进行这些运算十分繁复，通过借用复数表示正弦信号可以使正弦电路分析得到简化。
　　1. 正弦量的相量表示
　　构造一个复函数
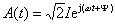
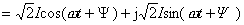
　　对 A(t) 取实部得正弦电流：
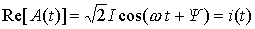
　　上式表明对于任意一个正弦时间函数都有唯一与其对应的复数函数，即：
　　　
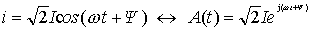
　　 A(t) 还可以写成
　　称复常数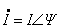为正弦量i(t)对应的相量，它包含了i(t)的两个要素I ,Y 。任意一个正弦时间函数都有唯一与其对应的相量，即：
　　　
　　注意：相量的模为正弦量的有效值，相量的幅角为正弦量的初相位。同样可以建立正弦电压与相量的对应关系：
　　例如若已知正弦电流和电压分别为：
　　
　　 则对应的相量分别为：
　　 若正弦电流的相量 频率
　　 则对应的正弦电流为：
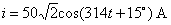
　 2. 相量图
　　 在复平面上用向量表示相量的图称为相量图。如已知相量
　　　　　　
　　 则对应的相量图如图1所示。辐角为零的相量称为参考相量。

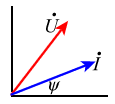图1

　3.相量法的应用

(1) 同频率正弦量的加减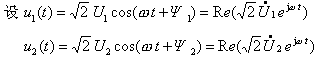
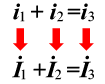则：	图 2
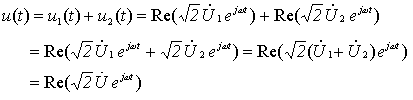从上式得其相量关系为：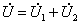
故同频正弦量相加减运算可以转变为对应相量的相加减运算，运算过程如图 2所示。

　　（2）正弦量的微分、积分运算
　　 设
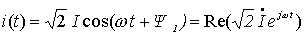
　　　 则
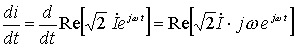
　　　 即 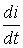对应的相量为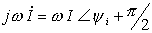
　　　 而
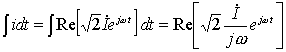
　　　 即 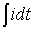对应的相量为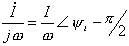
　 以上式子说明正弦量的微分是一个同频正弦量，其相量等于原正弦量i 的相量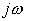乘以，正弦量的积分也是一个同频正弦量，其相量等于原正弦量 i 的相量除以。

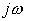例如图3所示 RLC 串联电路，由 KVL 得电路方程为 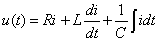　　　　 　根据正弦量与相量的关系得以上微积分方程对应的相量方程为 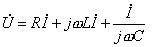　　　　 　 因此引入相量的优点是：
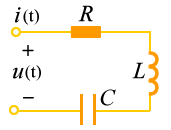	图3

　　 （1）把时域问题变为复数问题；
　　 （2）把微积分方程的运算变为复数方程运算；
　　需要注意的是：
　　 1）相量法实质上是一种变换，通过把正弦量转化为相量，而把时域里正弦稳态分析问题转为频域里复数代数方程问题的分析；
　　 2）相量法只适用于激励为同频正弦量的非时变线性电路。
　　 3）相量法用来分析正弦稳态电路。